median
don steward
mathematics teaching 10 ~ 16
don steward
mathematics teaching 10 ~ 16
Thursday, 31 March 2011
Wednesday, 30 March 2011
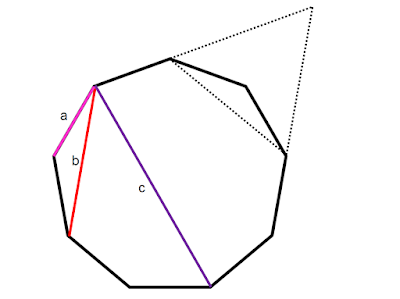
nonagon appreciation
a nonagon has several properties involving some nice simple angles
a ppt is here
show that a + b = c
Saturday, 26 March 2011
ring alignments
if you have a ring of regular pentagons
it takes 10 to complete a full loop
why is that?
if you have a ring of regular decagons
it also takes 10 to complete a loop
why is that?
then one seems to fit snugly inside the other
how come they align so neatly?
it takes 10 to complete a full loop
why is that?
if you have a ring of regular decagons
it also takes 10 to complete a loop
why is that?
then one seems to fit snugly inside the other
how come they align so neatly?
hexagon fractions
what fraction of the
hexagon is
the orange shape?
this work has been developed and discussed in detail by Derek Ball and Barbara Ball (MT March 2008)
the bottom right-hand picture is a useful starting place
folding bits inwards needs some additional justification - but is a helpful insight/start
the top left picture can also use this way of viewing (folding technique) to help establish the fraction
the other two pictures can be seen as repeated applications of this technique
hexagon is
the orange shape?
this work has been developed and discussed in detail by Derek Ball and Barbara Ball (MT March 2008)
the bottom right-hand picture is a useful starting place
folding bits inwards needs some additional justification - but is a helpful insight/start
the top left picture can also use this way of viewing (folding technique) to help establish the fraction
the other two pictures can be seen as repeated applications of this technique
pentagon angles
are they?
by symmetry the angles in the yellow triangles must be the same
how can you show that the angle in the blue triangle (b) also = a?
use these two equations (solve them) to show that a = b
Tuesday, 22 March 2011
Sunday, 20 March 2011
Saturday, 19 March 2011
directed number arithmetic sped up
the rules for combining directed numbers with addition and subtraction are probably too burdensome for memory so some awareness needs to be cultivated, over time
and dropbox versions here
many thanks to her
once some facility with negative number additions and subtractions has been attained, it is desirable to move towards automating (i.e. no need to think too much) these skills
this is an important step in the mathematics curriculum
many difficulties in algebra can sometimes seem more related to a lack of understanding of directed number techniques
my view is that sophisticated directed number calculators recognise types of sum and can apply a technique for that general type
presenting students with a sheet of sums, they can work together on grouping the sums by type, explaining that the result (answer) and numbers involved are not important - it's the signs that need to be focused on (the 'form'):
it may be better that students choose how to group these sums themselves, with plenty of discussion,
but another sheet has them already grouped by types:
and then consider and create general rules for getting results for each type of sum, for themselves
e.g. for type (c) "you subtract the smaller from the larger and give it the sign of the larger (because this 'wins')"
e.g. for type (e) "two minuses don't make a plus; one story could be: if I take £7 from you and then take £12 from you, I've taken £19 from you altogether"
they can also appreciate, after a while, that types can be 'collapsed' to other types
e.g. (e) to (b) and (g) to (a)
and here is a test!
Friday, 18 March 2011
house to square
but you don't need to
having decided where the point P goes
check that the angles and sides do actually create a square
Subscribe to:
Posts (Atom)