bigger shares?

this task is from Tony Gardiner (Extension Mathematics, beta)

comparing fractions

considered generally

primes using 0 to 9

this task is one of Tony Gardiner's

you can use deduction to sort out common properties of solutions (and to establish that there are three of them)

difference between combined functions

establishing a general rule for the second resource can be difficult, due to the four variables involved
and looking for reasons using general algebra may not help too much...

perhaps hint that "you might like to look at the multiplier (of x) minus 1" and then, having found a rule, see how it works algebraically

easily marked

also easily marked

some non-linear functions

multiplying mixed numbers

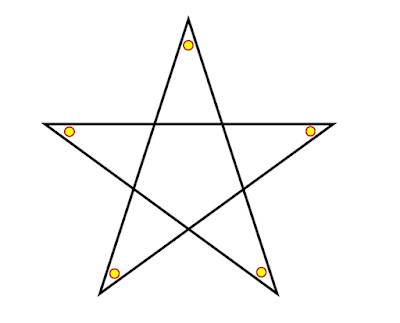
exterior angles and star polygons

the exterior angle of a regular polygon is the same as the angle that a circle is divided into

so the sum of the exterior angles must be 360 degrees














as an exercise in using exterior angles of regular polygons, students can be asked to find the angle sum of the pointed corners of the (n , 2) star polygon family

start with any vertex and join this to a vertex two places (i.e. next but one neighbour) round the circle
sometimes (when?) you get degenerate cases that fit together to make a star polygon (but this depends on your definition...)

a general rule for the angle sum for any number of sides of a regular star polygon can be deduced

there is a quick way of sorting out the angle sum for a regular pentagonal star

circle templates without centre points can be found at NRich

sector angles

it seems that it was the Babylonians who established the (arbitrary) idea that there are 360 degrees in a whole turn, linked to their base 60 arithmetic

there was an attempt to change this (in France) to 400 gradians (grads) to create a metric measure

once 360 degrees is established, the various fractions can be determined

this work is intended to be quick and, ideally, mental
what are the angles shown?

my apologies, the images that these are based on came from someone else
I failed to make a note of the source and couldn't find it again ... (?)

more (mental) work can focus on angles between numbers on the clock face and between the compass points

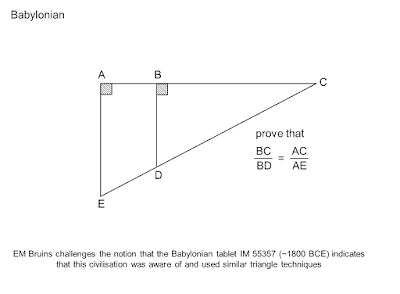
did the Babylonians use similar triangles?

IM55357 is a tablet showing right angled triangles

it is sometimes used as evidence that the Babylonians (around 1900 to 1600BCE) were able to use similar triangle techniques

EM Bruins points out that there is not widespread evidence of this being the case

he shows that a relationship can be derived just by using areas of triangles and a trapezium

how?

lunes

Hippocrates of Chios made some achievements with lunes on route to seeing if they could square the circle

maybe tell students that the semicircles have a side of a triangle as a diameter
maybe wait for them to ask
maybe they will assume that this is the case anyway...

following on from areas of circles (and Pythagoras' theorem) you can set your students two problems that are almost 2500 years old

mean of the means

finding the mean of the means for different sizes of subgroups is a way of practising this skill, subsumed within a larger task of establishing when the mean of the means is equal to the mean of the (parent) set

this happens evidently when the subsets are the same size

but... there are other cases when they are the same...

square is best

this work involves the area and perimeter of rectangles
(i) fixing the perimeter to be 16cm
(ii) fixing the area to be 36 carpet tiles
in this way two important functions (quadratic and reciprocal) can be considered
and number work practiced along the way...

the geogebra applet by Anthony Or is helpful, with a perimeter of 20 rather than 16