exterior angles and star polygons

the exterior angle of a regular polygon is the same as the angle that a circle is divided into

so the sum of the exterior angles must be 360 degrees














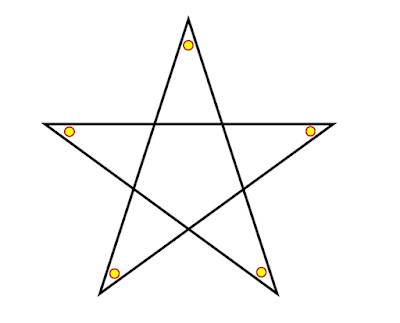
as an exercise in using exterior angles of regular polygons, students can be asked to find the angle sum of the pointed corners of the (n , 2) star polygon family

start with any vertex and join this to a vertex two places (i.e. next but one neighbour) round the circle
sometimes (when?) you get degenerate cases that fit together to make a star polygon (but this depends on your definition...)

a general rule for the angle sum for any number of sides of a regular star polygon can be deduced

there is a quick way of sorting out the angle sum for a regular pentagonal star

circle templates without centre points can be found at NRich