rearrangement add/take with times/share

with some confidence in dealing with addition/subtraction rearrangements and multiplication/division rearrangements separately, these operations can then be combined

hopefully students can relate 'undoing' steps to those involved in building the expression e.g.

'what happens to 3 in the first statement?' 

'doing':
you multiply it by 2
then add 4
so 'undoing' involves?
subtracting 4 first, then dividing by 2

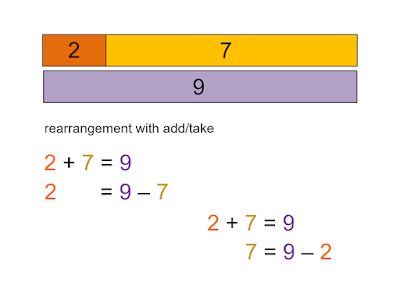
as with other rearrangement resources, these start with rearranging simple number statements (so that rearrangements can be checked for correctness) before moving to an involvement of symbols

a sense of appropriate transformations of a statement is built from an understanding of what happens with numbers (algebra as generalised arithmetic)

a powerpoint is here

equivalent statements
look different but still say the same thing

rearrangement times/share with letters

once some facility has been made using numbers in multiplication and division rearrangements, these techniques can be applied to equations/formulas with letters (symbolic forms)

a powerpoint is here

rearrangement times/share with numbers

‘doing the same to both sides’ and ‘balance’ models can help to emphasise the equality of two sides of an equation/formula but seem to me to be not easily assimilated ideas when compared to using inverses, in visual ways, when transforming a statement as a rearrangement

it may well be important to link the ideas of both models

in the case of multiplication/division, by starting from rearrangements of numerical statements  transformations can be appreciated as equivalent statements involving those particular numbers
(given this statement, we can also say this...) 

how these statements are deduced in terms of multiplying being the 'opposite' or inverse of division (and vice versa) can hopefully be appreciated - appealing to what happens visually

it seems helpful to focus on the 'shape' of a resulting transformation, compared with the initial statement e.g. top statement: 'the 3 is upstairs and it is multiply by' to: lower statement, 'the 3 is downstairs and it is divide by' 

a powerpoint is here

visuals of rearrangement

rearrangement add/take with numbers

intuitive knowledge about rearrangement can be obtained from simple number sentences and their equivalent forms, probably assisted by diagrams

objectivity can be established over time - by participating in discussion about the allowable transformations

my preference is to let students develop their own notions about rearrangements by presenting them with several (judiciously chosen) examples

I don’t think it is helpful to simply tell students that e.g.  ‘changing sides changes the sign’ because, however instrumentally effective, it is better that students notice and interpret information and build their own structural sense of techniques

students can and do note that signs change when they ‘move’ from one side of an equals sign to the other

they can hopefully relate this understanding to an appreciation of using the the helpful notion of inverses

the powerpoint is here

quadratic matchstick patterns

ducks nth term

these have perhaps a curious purpose...
find a general rule for the daffy ducks
find a general rule for the donald ducks
and find a general rule for both ducks, relating this to the diagrams

simple linear relationships

a simpler version of linear relationships

what (whole, positive) numbers can students find to fit these rules?

V-problems

it may be helpful for students to put the expressions on bits of paper - to be able to change the arrangement more easily

six legs

simpler versions of transformational spiders
thanks to Aimee and Dan (Telford and Wrekin primary school teachers), working on a Mathshub primary algebra project

geometric sequences, some with surds