powers of 3

how many ellipses at each stage?

thirds and fifths

[based on an idea from the AQA GCSE problem solving questions 2008]

two strips of card are 30cm long
one is divided into thirds
the other is divided into fifths

what are the total overall lengths for these three arrangements?

what other lengths can be made?
why must the overall lengths all be even?

establish that all but four even lengths between 30cm and 60 cm (inclusive) can be made in this way (by lining up two of the fraction marks)

trees, powers of 2

powers were invented for fractals

repeated addition = multiplication
repeated multiplication = powering (or maybe indicing?)

how many branches at the ends, as the tree grows?

powers of 5

 how many pentagons are there altogether?


















these look a bit weird:

sculpture by Tony Cragg

















how many squares at each stage:

square diamond

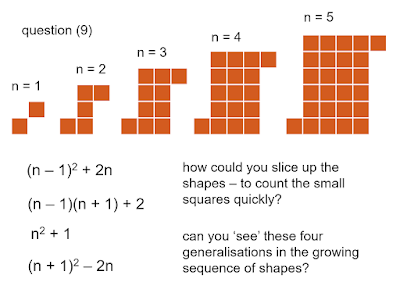
quadratic growing rules (ii)

a ppt is here

quadratic growing rules (i)

growing in two directions, across and up, (quadratic) sequences

a ppt is here

the growing sequences of shapes
have a quadratic nth term form

general rules can be established from the diagrams directly and also from factor pairs (they can be reformed into a rectangle)

or by other, algebraic methods...

part of the interest in generalising these growing sequences is in relating apparently different rules, from various 'viewings' of particular cases - that seem 'regular'

for example, question (4) above can have various nth term generlisations from different viewings:

regular polygon angles

how many regular polygons have an interior angle that is a multiple of 9?

the decagon is one such regular polygon, can you find and establish that there are just five others (i.e. six altogether)?