coordinates of an isosceles trapezium

three coordinates of an isosceles trapezium (trapezoid) are:
(1 , 3)
(-2 , 2)
(6 , -2)
what is the 4th coordinate?













prove that the resulting shape is an isosceles trapezium

9 isosceles trapeziums

what relationships must there be between the lengths of the sides of the isosceles trapezeium used so that 9 of them fit together to make an enlarged version of the shape?

and what must the angles be?

scatter and correlation

although there is value in plotting scatter graphs by hand, there is also value in using a spreadsheet to automatically draw a line of best fit and give its equation

people argue, generally rightly, that ICT can free up time to consider interpretations, evaluations and other analyses

using ICT, questions can be reversed: students could be asked to generate data sets with particular correlations

students could be asked to guess these,
following an understanding that the coefficient varies between -1 and +1

some scatter graphs with their correlations

multiplication = addition?

find other number pairs that work in a similar way

generalise

prove

division = subtraction?

can you find other sums so that replacing the division sign by a subtraction sign does not alter the result of the calculation?

can you find a general rule?

can you justify a general rule?

four digits, two fractions

font size and length

these font sizes (F) were
81   then 54   then 36   then 24   then 16

measure the lengths of the words (L) carefully

try to find a linear rule connecting the size of the font and the length of the word


[ printers will probably vary but, using a spreadsheet: L = 0.1563 F - 0.1047 ]

multiple puzzles

M(15) means the number must be a multiple of 15 i.e. 15 or 30 or 45 or 60 or 75 or 90
find four digits (all differenet) to go in each of the boxes to make 2-digit multiples of the required number when you read across and down:

fraction sequence

what is the nth term of this fraction sequence, which continues with a regular pattern?

prime sums

(1)  what is the total of the first nine prime numbers?

(2)  the primes bigger than 5 and less than 90 are put into threes and each of the totals of these trios are found
then these totals are reversed
what is the total of  (a) the original trios  (b) the reversals?

find the number

find the number from the given clues
[the numbers of factors include 1 and the number itself]

cake slices

as an example of inverse proportion,
suppose several fairly hungry people, who like blueberry cake, gather together

the cake is cut into 24 slices

if there is only one person present they can have all 24 slices
if there are 2 ...
if there are 3 ...
if there are 4, 6, 8, 12, or 24?

what does the graph show?

direct and inverse proportion

a ppt is here

approximate square roots

this isn't too helpful a technique, but does practice some useful skills

compare some actual square roots with the approximations, using the formula

quadrilaterals to a rectangle

the topic of area can be approached from a perspective that all shapes are really rectangles (pretending to be something else)

present the pictures to students and ask them to explain how a kite and and an arrowhead can be transformed  into rectangles of equal area:

and a rhombus:

Kobon triangles

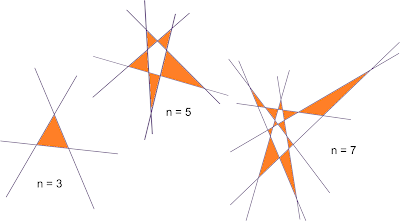
Kobon Fujimura posed the problem (fairly recently) of finding the maximum numbers of triangles (not overlapping) for a given number of straight lines.

Students could be asked to explore this, for up to 10 lines:

some diagrams for
n = 3 , 5 and 7 are shown, giving totals of
1 , 5 and 11 respectively

for n = 4 , 6 and 8 the totals are 2 , 7 and 16

can students produce diagrams for these?




beyond small numbers of lines the diagrams become complex, with tiny triangles
for solutions see e.g. Wolfram

 (there could be 26 for 10 lines)



some examples:

n = 9 giving 21 triangles

n = 10 (shown symmetrically) giving 25 triangles (it might be possible to produce 26)

n = 18

n = 20

















Saburo Tamura proved that an upper limit to the number of triangles is given by the largest integer less than or equal to
n(n - 2)/3

art work

factor links (factorgrams)

an arrow means that a number divides exactly into another number ('is a factor of')

in this work it needs to be fairly often repeated that all the arrows that can be drawn have been drawn 

so you cannot have a number that divides into another without there being an arrow to show this

start off with students drawing the arrows themselves:

draw all the arrows that you can to show the relationship 'is a factor of'

note that for question (1) you cannot use e.g. 3 and 6 since there is no arrow between the two blank circles (i.e. one must not be a factor of the other)

for this reason, you should not use 1 or the number itself