semicircle cutting

in a local factory one of the tasks was to cut out many semicircles, as lugs to be welded onto a drain hole cover

they cut these out with a laser in an obvious way:

is there a more efficient way to do this?

how might you compare these two and other arrangements?

there needed to be some distance between the shapes
otherwise the heat from the cutting process would warp the metal (say 2 mm gap)

incircle of a right angled triangle

by considering areas, you can establish that the radius of the incircle is
ab/(a + b + c)

by considering equal (bits of) tangents you can also establish that the radius,
 r = 1/2 (b + a - c):

b + a - c  =  (e + g) + (e + f ) - (g + f)  =  2e  =  2r

for integer values of the incircle radius you need a pythagorean triple

with the (subset of) pythagorean triples generated from the shortest side being an odd number

3, 4, 5  has an incircle radius, r = 1
5, 12, 13  has r = 2 (property for shapes where the area value = perimeter value, 'equable')
7, 24, 25  has r = 3
9, 40, 41  has r = 4
etc.

using the (pythagorean triple) property that a chosen odd number ('a') when squared is broken up into two consective integers for 'b' and 'c', you can (using some reasonably complicated algebra for the first relationship above) show that this pattern continues, for ever and ever....

for such pythagorean triples (and the statements are also true in general), you can also establish that
3 must be a factor of either a or b (but not both)
4 is a factor of a or b
5 is a factor of a, b or c

Benford's law

Frank Benford published a rule in 1938 (that had been identified by Simon Newcomb, in 1881) that if you look at a large enough sample of real data e.g. people's house numbers, around a third of the numbers will start with a 1





remarkably, the frequency of the numbers of digits, d, usually follows a log law:

F(d) = log(1 + 1/d)

values from this (theoretical) frequency distribution are shown above

students could see how this distribution compares with
real-life data
e.g.

• house numbers of people in their class or year group
• populations of cities in a country
• lengths of longest rivers in the world
• populations of countries in the world
• lead digits of several scientific constants 

the 'numberphile' youtube clip

faces on a cube

this is the same cube, seen from three different positions
which faces are opposite to each other?

regular octagon?

from an MEI question

sum of the squares

David Wells suggests reforming the formula for summing square numbers:

to the more symmetrical:

daisy

this problem appeared in one of Brian Bolt's books*
it's promoted a keen interest in getting from 1 up to the highest number
but it's daunting to check repeatedly...

the task is to try to be able to make all numbers from 1 up to as high a number as you can

you put any six numbers in the regions (yes, there could be repeats)

you can only add up numbers in regions that are adjacent (have a common border)

you can only add in a number from a region once

for example, with a 1 in the centre:

a fairly low
highest number
but you can make all the numbers from 1 up to 25

note that 10 is not 4 + 6 because those regions are not adjacent










another example, if 18 is in the middle and 1 , 2 , 4 , 5 , 5 round the outside (in this order) then you can make from all numbers from 1 up to 35

there's an interesting consideration about whether to place a small number in the centre (for versatility) or a large number (to get to bigger numbers)

in the solution section of Brian's book it gives 43 as a highest total
this was beaten by trainee teacher in 1996 who got up to 45
then this record was beaten, also in 1996, by an 11 year old who spent a lot of time on it at home - who got from 1 to 46

nrich ran this activity on their website and 46 was the highest number submitted

the easier-to-play-around-with versions are also quite interesting:

for:

• 2 pieces, the highest is 3
• 3 pieces, the highest is 7
• 4 pieces, there are two different solutions that give from 1 to 13
• 5 pieces, the highest is 19
• 6 pieces gives 1 to 27
• 7 pieces, I make 1 to 33
• 8 pieces, I make 1 to 41

then I gave up...

* 'a mathematical pandora's box', by Brian Bolt

maxi pyramid

you obtain a value from the two immediately below it

the rules for forming a pyramid are quite complex:

(a) the five bottom numbers must sum to 20
(b) for now, no zeroes are allowed
(c) if the two numbers are even you add them to get the one above
(d) if the two numbers are odd you take the smaller from the larger to get the one above
(e) if there is one of each (odd with an even) you multiply the two numbers to get the one above

what is the largest top number you can obtain?

it is easy to overlook one of these rules, especially the bottom numbers needing to sum to 20

the highest (world record) so far, without using zeroes, is 226
if zeroes are allowed, the record so far is 300
if negative numbers are allowed you can make huge top numbers

[ task devised by Ian Sugarman when he worked at the Shropshire Maths Centre ]

distances from five numbers

given five numbers: e.g. 3 , 7 , 9 , 2 , 5
choose any other number and work out the sum of the (positive) distances from this number

e.g. if I choose 4, the sum is 1 + 3 + 5 + 2 + 1 = 12

explore the sums of distances from various points
when is this distance a minimum?

try to give a reason why this is true

you are not restricted to the range of numbers given - you could choose to start from e.g. 11
what happens when you move away outside the range of the given numbers?
why?

try starting from another set of five numbers
or more
or less

weighty averages

for some reason, you have many weights but they are all either 3kg or 8kg

how can you get a mean of
(i) 4kg?
(ii) 6kg?
(iii) 4.5kg?
(iv) 6.9kg?

you can also explore other pairs of weights and different means to create with these

2 consecutive heads

ask students to keep throwing a coin until they get two heads in a row
how many throws does it take to get two heads in a row?

do this several times







from the experimental data, possibly collected from the class, what is the average expected number of throws until you get 2 heads in a row?

the expected value is 6
and this theoretical value can be compared with the (average) of the experimental values obtained

how widely do the experimental values vary?

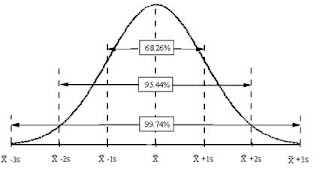
standard deviation

this routinely used (sophisticated) measure of the spread of a distribution doesn't feature (currently) in the English maths national curriculum - which seems a shame

it is, sensibly, in the Scottish curriculum












these small data sets have the same mean (of 11) and integer standard deviations

they can be useful for students to work through the steps of the calculations, considering why the steps make (some) sense

averaging

choose any two numbers

the next number is the average of these two
the next is the average of the last two
etc.

students can explore the limit - which is reached fairly quickly

the limit is a linear combination of the first two terms

this has been called 'Littov's chain' but someone (Raz Lamplugh) told me this was a made up name...

it generalises to e.g. choose any three numbers then repeatedly work out the average of the previous three numbers

multiples of 36

using 5, 6 and 7 as three digits of a four digit multiple of 36,

find the largest and also the smallest (4-digit) number

[you should find that the difference between them is 4680]


can you also find a multiple of 36 with three 8s in it?




[ this problem was posed by Tony Gardiner ]

multiple of 27

using all of the digits 3, 4, 5 and 6
in a 4-digit number,
find all nine (4-digit) multiples of 27

number chain

d(23)

let's call two numbers d(23) if

a x b - (a + b) = 23

the task is to find two numbers so that the difference between the product and the sum of these is 23

can students find the four pairs of integers ('a' and 'b') that fit this rule?

can they find some rational solutions?


the intention of this task is that students substitute numbers by trial and improvement
and hopefully appreciate the symmetry of results

however, if they were to add 1 to both sides
the problem is solved quite simply,
algebraically,
by factorising

trapezium bit areas

any trapezium (trapezoid)
with the two diagonals

why must the orange (left) and yellow (right) triangles have the same area?

if the bottom (base) of the trapezium is double the length of the top,
and because the triangles are similar
what is the relationship between the areas of the top (gold) and bottom (light red) triangles?
[it is 4 times bigger]

so, what fraction of the whole trapezium area is the top (gold) little triangle?

what if the base is treble the top?
etc.

in general, if the bottom length is 'k' times longer than the top length,
show that the orange and yellow triangles are (each)
k times the area of the top (gold) triangle

[a bit tricky]

fibonacci trapeziums (trapezoids)

how many triangles in the trapeziums?

how do these relate to the Fibonacci sequence?

does this pattern continue?

why is that?

polygon angles

this dissection suggests a rule that might be easier to appreciate than drawing diagonals from one corner

it is also the method that Euclid appears to have chosen (as a corollary to the angles in a triangle summing to 180 degrees)

the angle sum for an 'n' sided polygon is
n x 180 - 360 

at each vertex the interior angle + exterior angle  = 180

if there are 'n' sides then the sum of the exterior angles plus the interior angles = 180n

as the sum of the interior angles is (n - 2) x 180 so the sum of the exteriors must be 360 to make the total of 180n

right triangle using 1 to 7

use 1 to 7, once only, so that the lines have the same total 

prove that the line totals cannot be below 12 or above 15 

prove that a line total of 14 is impossible

there are two solutions for sum = 13 and one for sums of 12 and 15 

students can be asked to find all of the solutions, once they have luxuriated in the glory of finding one solution of course...

hard haitch using 1 to 7

use 1 to 7 so that the (four) lines of three all add up to the same number

prove that 4 must go in the middle and the only possible total is 12


there are three solutions but these (maybe trivially) involve switching numbers within the lines of three

Zorro using 1 to 7

use digits1 to 7 (once only) so that the lines of three have the same total

what totals are possible and how many variants are there? 

prove that the middle must be even

prove that 7 and 6 must not be in the same line









ignoring unimportant swaps, show that there are: 

• two solutions with 2 in the middle
• three with 4 in the middle 
• two with 6 in the middle

prove that only totals of 11, 12 and 13 are possible

why is a total of 14 impossible?

this is the same as a task called 'Haitch'
Graeme Brown produced an Excel interactive version to download for nrich here

                                                                                                                               

cyclic quadrilateral angles

show that if the angles in a quadrilateral are in a linear growing sequence (i.e. in arithmetical progression) then it must be cyclic

while you're at it, show that such angles must either all be even or all odd