it is from Pat's blog (Pat Ballew, Kentucky, USA)
and has some neat extensions
a powerpoint
you can begin this application of Pythagoras task by asking students to draw a square inside another square on a dotty grid
then join the corners in a "windmill" manner - that really needs to be demonstrated
(and needs to be done in a regular way)
or ask them what is happening:
(mine is different to Pat's...)
students could find as many options as they can on 7 by 7 (or is it 6 by 6) dotty grids
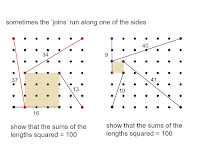
and some options can be presented to show that the 'inside' square could have a length (or two) on the perimeter of the larger square
sometimes you can find pairs that have the same total
maybe give sheet (a) to one student and sheet (b) to another
their solutions should be the same (but in a different order)











No comments:
Post a Comment